e-ISSN 3073-1151 | Edición Octubre-Diciembre, 2024
Volumen 1 | Número 4 | Páginas 202-212
Estrategia pedagógica del aprendizaje basado en proyectos en la enseñanza de estadística y probabilidad.
Pedagogical strategy of project-based learning in the teaching of statistics and probability.
Joffre Hernán Pineda Procel[1] 
, Jhonny Alfredo Alban Alcívar[2] , José Yovany Cañar Cuenca[3] , Hernán David Jiménez Ordóñez[4] , Diego Andrés Quezada Yaguachi[5]
|
INFORMACIÓN DEL ARTÍCULO
Historial del artículo Recibido el 06 de noviembre de 2024 Aceptado el 04 de diciembre de 2024 Publicado el 11 de diciembre de 2024
Palabras clave: aprendizaje basado en proyectos, estadística, probabilidad, educación básica, razonamiento lógico
ARTICLE INFO
Article history: Received November 6, 2024 Accepted December 4, 2024 Published December 11, 2024
Keywords: project-based learning, statistics, probability, basic education, logical reasoning |
RESUMEN
Este estudio evalúa la implementación del Aprendizaje Basado en Proyectos (ABP) como estrategia pedagógica en la enseñanza de estadística y probabilidad para estudiantes de 5to año de Educación General Básica. La investigación compara los resultados de un grupo experimental, que utilizó la metodología ABP, con un grupo control que continuó con métodos tradicionales. Se empleó el Test de Lawson para medir el razonamiento lógico-matemático antes y después de la intervención. Los resultados muestran un incremento significativo en el rendimiento del grupo experimental, evidenciando mejoras en la comprensión de conceptos estadísticos y probabilísticos, así como en el desarrollo del pensamiento crítico. El análisis de datos se realizó mediante la prueba U de Mann-Whitney, confirmando la efectividad del ABP frente a los métodos tradicionales. La investigación muestra la relevancia de integrar enfoques prácticos y basados en situaciones reales en la enseñanza de las matemáticas.
ABSTRACT
This study evaluates the implementation of Project-Based Learning (PBL) as a pedagogical strategy in the teaching of statistics and probability for 5th year students of General Basic Education. The research compares the results of an experimental group, which used the PBL methodology, with a control group that continued with traditional methods. The Lawson Test was used to measure logical-mathematical reasoning before and after the intervention. The results show a significant increase in the performance of the experimental group, evidencing improvements in the understanding of statistical and probabilistic concepts, as well as in the development of critical thinking. Data analysis was performed using the Mann-Whitney U test, confirming the effectiveness of PBL compared to traditional methods. The research shows the relevance of integrating practical and real-life approaches in the teaching of mathematics.
© 2024 Pineda Procel, J. H., Alban Alcívar, J. A., Cañar Cuenca, J. Y., Jiménez Ordóñez, H. D., & Quezada Yaguachi, D. A.
Esta obra está bajo una licencia internacional |
Introducción
La estadística en América Latina es parte del currículo de matemáticas en 5.º y 6.º grado de la educación primaria; sin embargo, su enseñanza ocupa un porcentaje limitado del tiempo en el aula. Se estima que solo el 16 % del tiempo dedicado a las matemáticas aborda esta disciplina. Por ello, es fundamental fortalecer su enseñanza en esta etapa educativa. Esto no debe limitarse a la interpretación de tablas y gráficos, sino que también debe incluir la resolución de problemas que impliquen análisis de datos, promoviendo un aprendizaje más integral y práctico (López, 2015).
El ABP ofrece un enfoque altamente efectivo para la enseñanza de estadística y probabilidad, ya que fomenta la participación de los estudiantes en la resolución de problemas reales y aplicables a su entorno. El ABP promueve la colaboración en pequeños grupos y permite que los estudiantes se apropien de su proceso de aprendizaje al investigar y aplicar los conceptos clave de estadística y probabilidad en situaciones auténticas, como el análisis de encuestas, la interpretación de gráficos o el cálculo de probabilidades en experimentos cotidianos (Penalva et al., 2010).
Esta metodología activa no solo favorece el aprendizaje autónomo y colaborativo, sino que también estimula la comprensión profunda de los conceptos a través de un enfoque práctico y contextualizado. Los problemas planteados en ABP permiten que los estudiantes exploren ideas previas, introduzcan nuevas variables y transfieran sus aprendizajes a diferentes contextos. Esto facilita que los estudiantes desarrollen una comprensión más integral y significativa de la estadística y probabilidad, conectando lo aprendido con el mundo real y fortaleciendo su capacidad para razonar de manera lógica y crítica (Espinoza y Sánchez, 2014).
La enseñanza de la estadística en la educación primaria permite desarrollar en los estudiantes la habilidad de recolectar, organizar, analizar e interpretar datos, y considerando el aumento exponencial de la digitalización y los grandes volúmenes de datos e información que esto genera, conocer acerca de la estadística se convierte en una herramienta valiosa para comprender el mundo que les rodea y tomar decisiones adecuadas. Como señala Franklin et al. (2007), 'la educación estadística fomenta el razonamiento crítico y la capacidad de tomar decisiones informadas, competencias esenciales en una sociedad impulsada por datos'. Asimismo, Godino (2011) destaca que 'la estadística en la educación básica es fundamental para desarrollar una ciudadanía crítica capaz de interpretar y cuestionar la información presentada en diversos contextos'.
Por otra parte, la enseñanza de la probabilidad en la educación primaria ha tomado relevancia en los currículos de diversos países, no obstante, sigue siendo un desafío tanto para los docentes en formación como para los ya en ejercicio. El estudio de la probabilidad conlleva conocer y entender conceptos básicos probabilísticos como lanzar una moneda o tirar un dado para luego aplicar estos conocimientos al mundo real. Esto fomenta el desarrollo del pensamiento lógico ayudándoles a entender que el azar tiene patrones y que esto puede ser objeto de estudio (Vásquez y Alsina, 2014).
Como se puede apreciar a partir de los aspectos señalados previamente, hay diferentes puntos de vista de la problemática principal, lo que conlleva a plantearnos en esta investigación sobre la dificultad que los estudiantes presentan al comprender y aplicar conceptos estadísticos y probabilísticos en contextos prácticos. A menudo, los métodos tradicionales de enseñanza se enfocan en la memorización de fórmulas y procedimientos, lo que limita la capacidad de los estudiantes para aplicar estos conocimientos de manera significativa.
Este enfoque tradicional no siempre favorece el desarrollo de habilidades de razonamiento crítico, lo que deja a muchos estudiantes con un conocimiento superficial y desconectado de las aplicaciones reales de la estadística. La falta de una comprensión profunda de estos conceptos afecta no solo su desempeño académico, sino también su capacidad para tomar decisiones informadas basadas en datos, una habilidad crucial en el mundo moderno (Bueno, 2018).
En respuesta a esta problemática, esta investigación plantea la implementación del ABP como una estrategia pedagógica que permita mejorar la comprensión de la estadística y la probabilidad en los estudiantes de tres paralelos del 5to año de Educación General Básica de la Unidad Educativa Particular Bilingüe "Principito & Marcel Laniado de Wind", para esto se ha propuesto evaluar el impacto del ABP en la comprensión y aplicación de los conceptos de estadística y probabilidad e identificar los cambios en la actitud de los estudiantes hacia estas materias.
Metodología y materiales
La metodología de investigación utilizada en este estudio se enmarca en el paradigma cualitativo interpretativo no experimental, con un diseño de grupos controlados. La temporalidad es transversal, y se basa en la implementación del ABP en la enseñanza de estadística y probabilidad. El análisis se realizó utilizando la prueba U de Mann-Whitney para evaluar las diferencias entre el grupo experimental y el grupo control, empleando el Test de Lawson como instrumento de evaluación del razonamiento lógico-matemático.
El enfoque se centra en comprender cómo los estudiantes del 5to año de Educación General Básica de la Unidad Educativa Particular Bilingüe "Principito & Marcel Laniado de Wind" se adaptan a la enseñanza de la estadística y la probabilidad mediante la implementación del ABP. Lo que se busca es analizar de qué manera la aplicación de esta estrategia influye en su comprensión y en la adquisición de competencias matemáticas.
El estudio utilizó un diseño de grupos controlados, donde los estudiantes fueron divididos en dos grupos: un grupo experimental, que recibió la intervención pedagógica basada en el ABP, y un grupo control, que continuó con las estrategias tradicionales de enseñanza (Espinoza y Sánchez, 2014). La selección de los estudiantes fue aleatoria y se aplicaron pruebas pretest y post-test utilizando el Test de Lawson como instrumento de evaluación, tanto antes como después de la intervención.
Instrumento de recogida de información:
El Test de Lawson diseñado para evaluar el razonamiento científico y matemático, consta de 24 ítems que permiten medir la capacidad de los estudiantes para aplicar conocimientos en lugar de repetir definiciones. Estos ítems están organizados en 12 pares de preguntas, en las que cada una va seguida de una segunda que requiere la justificación de la respuesta inicial.
Para considerar una respuesta como correcta, tanto la respuesta como su justificación deben ser precisas, es decir, deben resolver adecuadamente el problema planteado. Los resultados del test permiten clasificar a los estudiantes en tres niveles de razonamiento: a) Concreto: en este nivel, los estudiantes utilizan razonamientos empíricos y deductivos, pero no logran contrastar hipótesis; b) Transición (intermedio): los estudiantes son capaces de identificar hipótesis causales no observables, lo que significa que pueden razonar a partir de proposiciones, formular hipótesis y probarlas; y c) Formal: los estudiantes en este nivel son capaces de validar hipótesis causales tanto observables como no observables, y ponerlas a prueba. El test ha sido adaptado y validado, y su confiabilidad total alcanza un valor de 0,88 según el coeficiente Alpha de Cronbach.
Muestra
La muestra estuvo compuesta por 78 estudiantes de 5to año de Educación General Básica de la Unidad Educativa Particular Bilingüe "Principito & Marcel Laniado de Wind," distribuidos equitativamente en dos grupos: experimental y control. Cada grupo incluyó a 39 estudiantes, repartidos en tres paralelos. El paralelo A y el paralelo B contaron con 14 estudiantes en cada grupo, mientras que el paralelo C estuvo conformado por 11 estudiantes en ambos grupos, lo que garantiza la representatividad y balance entre los grupos para el análisis comparativo.
Análisis de los datos
El análisis de datos se realizó utilizando el software estadístico IBM SPSS Statistics, aplicando la prueba no paramétrica U de Mann-Whitney, siguiendo los procedimientos metodológicos adecuados para garantizar la validez de los resultados. Esta prueba permitió identificar posibles diferencias significativas entre los grupos experimental y control en función de un mismo instrumento de evaluación, el Test de Lawson (Cohen y Manion, 1990). Como lo señala Hernández-Sampieri (2014), 'el uso de pruebas estadísticas adecuadas permite interpretar de manera precisa las diferencias entre grupos, garantizando la objetividad y validez de los resultados obtenidos'.
La investigación cumplió con los estándares éticos establecidos, obteniendo el consentimiento informado de los participantes, asegurando la confidencialidad de sus datos y garantizando su participación voluntaria. Además, se evitó cualquier exposición a riesgos físicos o psicológicos durante el desarrollo del estudio. Como lo señala Bernal (2016), el respeto a los principios éticos en la investigación no solo protege los derechos de los participantes, sino que también refuerza la validez y credibilidad de los resultados al garantizar prácticas responsables y transparentes.
Metodología Implementada en el Aula
Previo a la implementación de la metodología ABP, pedagógicamente es beneficioso proporcionar a los estudiantes una reseña o introducción a los temas claves de estadística y probabilidad, esto con el fin de proporcionar un marco de referencia el cual les permitirá comprender mejor cómo aplicar lo que saben a la resolución de problemas. Según Díaz-Barriga (2013), proporcionar un contexto inicial o marco de referencia antes de introducir metodologías activas como el Aprendizaje Basado en Problemas (ABP) facilita la comprensión y promueve el desarrollo de habilidades cognitivas necesarias para la resolución efectiva de problemas.
Los contenidos para el desarrollo e implementación de la metodología ABP son los descritos en la Tabla 1 y Tabla 2.
Tabla 1. Conceptos Fundamentales de Estadística y su Implementación en ABP
|
|
N° |
Contenidos |
Descripción Pedagógica |
Aplicación Metodológica en ABP |
|
1 |
Proceso estadístico y tablas de frecuencias |
Los estudiantes aprenderán a organizar y clasificar datos utilizando tablas de frecuencias. Se enseña cómo recolectar datos, agruparlos y presentarlos de manera comprensible. |
Los estudiantes aplicarán este proceso en la recolección de datos en proyectos ABP, como encuestas entre compañeros sobre temas de interés (ej. mascotas, deportes, juegos). |
|
|
2 |
Diagramas de barras |
Introducción a la representación gráfica de datos categóricos utilizando diagramas de barras. Se enseña cómo crear gráficos que muestren claramente la frecuencia de los datos. |
Durante los proyectos ABP, los estudiantes utilizarán diagramas de barras para representar los resultados de encuestas o experimentos (ej. número de libros leídos por semana).
|
|
|
3 |
Medidas de tendencia Central Media, Mediana y Moda |
Explicación sobre cómo calcular las medidas de tendencia central de un conjunto de datos. |
Los estudiantes usarán estos conceptos para analizar los datos de sus encuestas, por ejemplo, identificando la cantidad más común de horas de juego o la mediana de mascotas. |
|
|
4 |
Aplicación de programas informáticos |
Introducción al uso de herramientas tecnológicas, como hojas de cálculo (Excel), para realizar cálculos estadísticos y crear gráficos. |
Los estudiantes pueden usar programas informáticos para organizar y representar sus datos de forma más eficiente, facilitando los cálculos en sus proyectos ABP. |
Nota: Autoría propia.
Tabla 2. Conceptos Fundamentales de Probabilidad y su Implementación en ABP
|
|
N° |
Contenidos |
Descripción Pedagógica |
Aplicación Metodológica en ABP |
|
1 |
Combinaciones simples |
Enseñar las combinaciones simples y su cálculo. Los estudiantes aprenderán a contar los resultados posibles en situaciones sencillas. |
En proyectos ABP, los estudiantes pueden calcular combinaciones en situaciones como elegir diferentes sabores de helado o combinaciones de ropa para un día específico. |
|
|
2 |
Experiencias y sucesos |
Introducción a los conceptos de evento (suceso que puede ocurrir) y experimento (actividad que genera un resultado aleatorio). |
Los estudiantes llevarán a cabo experimentos sencillos como lanzar monedas o dados, y registrarán los resultados para analizar qué eventos ocurren con mayor o menor frecuencia. |
|
|
3 |
Noción de eventos y experimentos |
Explicación sobre los tipos de eventos (simples y compuestos) y cómo ocurren en experimentos. |
Los estudiantes aplicarán estos conceptos en sus proyectos, como al calcular la probabilidad de sacar una bola roja de una caja con diferentes colores de bolas. |
|
|
4 |
Experimentos aleatorios |
Introducción al concepto de aleatoriedad, donde el resultado de un experimento no puede predecirse con certeza. |
Los estudiantes realizarán experimentos como lanzar monedas o dados, registrarán los resultados, y discutirán la aleatoriedad de los resultados obtenidos. |
|
|
5 |
Cálculo de la probabilidad de un evento |
Enseñar a calcular la probabilidad de eventos simples (P(A) = resultados favorables / total de resultados posibles). |
Durante el ABP, los estudiantes aplicarán estos cálculos para determinar la probabilidad de sacar una carta de cierto color de una baraja o de ganar un premio en una rifa. |
Nota: Autoría propia.
Para implementar la metodología del ABP, el primer paso fue tener todo el material listo para promover el autoaprendizaje de los estudiantes como bibliografía virtual, libros físicos y material audiovisual, luego se procedió a organizar y dividir los grupos de trabajo y con ello, se comenzaron a realizar actividades que introdujeran a los estudiantes en el trabajo colaborativo. A cada grupo se les presentó un problema que debían resolver utilizando la metodología ABP.
Para la correcta implementación de esta estrategia de ABP se consideró elementos del método de los 7 pasos investigados por la escuela de Maastricht (Schultz y Christensen, 2004) a continuación se muestra la siguiente gráfica de la secuencia de los pasos a seguir:
Figura 1. Pasos a seguir para resolver un ABP
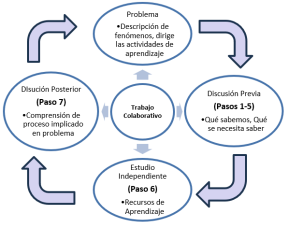
Fuente: (Espinoza y Sánchez, 2014).
Una vez que los estudiantes comprenden los conceptos, contenidos y procedimientos necesarios, se les asigna un problema o caso práctico para resolver en grupos colaborativos, utilizando materiales didácticos como libros, artículos web y recursos audiovisuales. Durante la intervención, trabajaron en problemas como la probabilidad de obtener un premio en una rifa, los resultados posibles en lanzamientos de dados, una encuesta sobre las mascotas que tienen en casa, la probabilidad de extraer una carta de cierto color de una baraja, el conteo de libros en casa y una encuesta sobre la cantidad de horas que dedican al juego.
Veamos cómo se desarrollaron los dos primeros problemas planteados e implementados en el proceso del desarrollo del trabajo de aula con problemas de ABP en grupos colaborativos:
Problema Nº1: Probabilidad de obtener un premio en una rifa
Una escuela organiza una rifa entre los estudiantes. Se han vendido 100 boletos, y solo 5 de ellos serán premiados. Los estudiantes deben calcular las probabilidades de obtener un premio si compran diferentes cantidades de boletos.
Tabla 3. Estructura del trabajo áulico del Problema 1
|
Cuestionario |
¿Cuál es la probabilidad de ganar si compras solo 1 boleto?
¿Cómo cambia la probabilidad si compras 5 boletos?
¿Qué tan probable es que alguien que compró 10 boletos gane? |
|
Logros por alcanzar |
Entender cómo se calcula la probabilidad en situaciones cotidianas como una rifa.
Analizar cómo varía la probabilidad al cambiar las variables (número de boletos comprados) |
|
Puesta en Común |
Los estudiantes discutirán los métodos usados para calcular las probabilidades, identificando tanto conocimientos previos como nuevos conceptos. |
|
Plan de acción |
Los grupos realizarán cálculos con diferentes escenarios, evaluando cómo el aumento en la cantidad de boletos afecta la probabilidad de ganar. |
|
Actividades de Aprendizaje |
Exploración: Los estudiantes realizarán cálculos simples para determinar las probabilidades. Crear una tabla que muestre cómo varían las probabilidades en función de los boletos comprados.
Introducción de variables: Buscarán información sobre probabilidad condicional para comprender mejor el impacto de la compra de varios boletos.
Síntesis: Crear un gráfico que muestre cómo la probabilidad cambia según el número de boletos comprados.
Transferencia: Aplicar los conceptos aprendidos a otras situaciones, como sorteos o juegos de azar. |
Nota: Autoría propia.
Problema Nº2: Probabilidad de lanzamientos de dados
Los estudiantes lanzan un dado 20 veces y deben registrar los resultados. Luego, calcularán las probabilidades de obtener cada número y compararán los resultados con las probabilidades teóricas.
Tabla 4. Estructura del trabajo áulico del Problema 2
|
Cuestionario |
¿Qué probabilidad tiene un estudiante de obtener un 6 en un lanzamiento?
¿Cuál es la probabilidad de obtener un número impar?
¿Coinciden los resultados reales con las probabilidades teóricas? ¿Por qué pueden diferir? |
|
Logros por alcanzar |
Distinguir entre probabilidad teórica y probabilidad experimental.
Entender cómo funcionan los eventos independientes en los lanzamientos de dados. |
|
Puesta en Común |
Los estudiantes compartirán sus resultados y analizarán las diferencias entre las probabilidades teóricas y los resultados obtenidos. |
|
Plan de acción |
Los estudiantes se dividirán en roles para registrar los resultados, calcular probabilidades y comparar con los resultados esperados. |
|
Actividades de Aprendizaje |
Exploración: Los estudiantes realizarán lanzamientos de dados y calcularán la frecuencia de cada resultado.
Introducción de variables: Investigar las diferencias entre probabilidad teórica y experimental, utilizando gráficos para representar los datos.
Síntesis: Crear una tabla que muestre los resultados y analizar patrones.
Transferencia: Aplicar lo aprendido en otros contextos, como el análisis de juegos con probabilidades similares. |
Nota: Autoría propia.
Resultados
En esta sección se presentan los resultados de la investigación en donde se presentan los análisis de los datos recolectados y los resultados cuantitativos obtenidos mediante la prueba de U de Mann-Whitney.
A continuación, se presentan los resultados obtenidos a través del Test de Lawson, en donde las gráficas muestran la distribución de los estudiantes en tres niveles de razonamiento: concreto, intermedio y formal, en los momentos de pretest y postest. Este análisis nos permite evaluar el impacto de la metodología ABP en la evolución del razonamiento lógico-matemático de los estudiantes, comparando los cambios en ambos grupos.
Figura 2. Niveles de Razonamiento Pretest y Postest
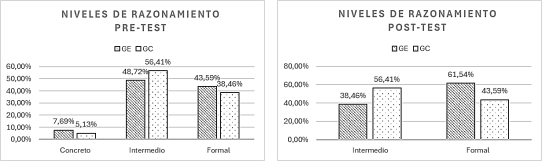
En el pretest, los estudiantes de ambos grupos se distribuyeron principalmente en los niveles intermedio y formal, con una baja proporción en el nivel concreto. Sin embargo, tras la intervención, se observa un cambio significativo en el grupo experimental, donde el porcentaje de estudiantes que alcanzaron el nivel formal aumentó de manera considerable de un 43.59% a 61.54%, mientras que en el grupo control este porcentaje se mantuvo prácticamente igual. Por otro lado, el grupo experimental mostró una disminución en el nivel intermedio, lo que indicaría una mejora en la capacidad de los estudiantes para formular y validar hipótesis, ver figura 3.
A continuación, se muestran los promedios alcanzados por los estudiantes de los tres paralelos A, B y C, permitiendo observar la evolución en su rendimiento. El análisis comparativo entre el pretest y el post-test en ambos grupos nos proporcionará una visión clara sobre el impacto del ABP en el grupo experimental, en contraste con los resultados obtenidos en el grupo control, que continuó utilizando métodos tradicionales de enseñanza.
Figura 3. Promedios Pretest y Postest en Grupos Experimental y Control por Paralelo
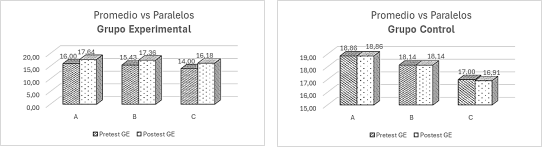
Se observa una tendencia diferenciada en los promedios de pretest y postest en los tres paralelos A, B y C. En el Grupo Experimental, los paralelos muestran un ligero incremento en el promedio después de la intervención pedagógica, el paralelo A pasa de un promedio de 16,00 en el pretest a 17,64 en el postest, los paralelos B y C también evidencian aumentos, aunque de menor magnitud, reflejando la efectividad general de la metodología aplicada. En el Grupo Control, los resultados presentan un comportamiento diferente, los promedios en los tres paralelos A, B y C permanecen prácticamente sin cambios entre el pretest y el postest. En el paralelo A, el promedio se mantiene en 18,86, mientras que, en el paralelo B y C, los cambios aparentemente son insignificantes.
|
Estadísticos de Prueba |
||
|
|
GE |
GC |
|
U de Mann-Whitney |
540,500 |
673,500 |
|
Z |
-2,214 |
-,875 |
|
Sig. asintótica(bilateral) |
,027 |
,381 |
Tabla 5. Prueba U de Mann-Whitney
Nota: Autoría propia.
Se observa claramente que en el grupo experimental (GE) en donde hubo intervención con la metodología ABP se evidenciaron cambios significativos en los promedios por cada paralelo, así como lo indica la prueba estadística U de Mann Whitney (
). Por otra parte, en los estudiantes en donde hubo intervención con la metodología actual, el grupo de control (GC), no se evidenciaron cambios estadísticamente significativos (
.
Discusión
La implementación de la metodología ABP en la enseñanza de estadística y probabilidad en estudiantes de 5to año de Educación General Básica produjo cambios significativos en la comprensión de los conceptos matemáticos clave. La comparación entre el grupo experimental en donde se implementó la metodología ABP, y el grupo control, que continuó con métodos tradicionales, dejó en evidencia que el enfoque ABP favoreció un aprendizaje más profundo y aplica-do. De este modo, se confirma lo señalado por Bueno (2018), quien destaca la importancia de reforzar la enseñanza de la estadística a través de metodologías que promuevan el análisis y la interpretación de datos en situaciones cotidianas. Vargas et al. (2021) sostienen que el ABP también fomenta el desarrollo de habilidades críticas y colaborativas, lo cual es esencial para preparar a los estudiantes frente a problemas matemáticos en contextos reales.
A pesar de los resultados favorables obtenidos en el grupo experimental, no debe soslayarse que la transición hacia un enfoque más activo y colaborativo en la enseñanza requirió un proceso de adaptación tanto para los estudiantes como para los docentes. Si bien los resultados del Test de Lawson muestran mejoras significativas en el razonamiento matemático de los estudiantes del grupo experimental, es preciso señalar que este impacto positivo no se limitó únicamente al dominio de los contenidos, sino también al desarrollo de habilidades de razonamiento lógico y crítico. Barrera Mesa et al. (2017) destacan que la integración de proyectos colaborativos mediados por TIC no solo potencia el aprendizaje de conceptos estadísticos, sino que también fomenta el trabajo en equipo y el pensamiento crítico, habilidades fundamentales para afrontar los desafíos del siglo XXI.
En contraste, el grupo control no evidenció cambios significativos, lo cual indicaría que los métodos tradicionales de enseñanza no logran generar los mismos niveles de participación y comprensión profunda que fomenta el ABP. Los resultados de esta investigación promueven la idea de que la enseñanza de las matemáticas, particularmente la estadística y la probabilidad, debe incorporar enfoques que conecten los contenidos académicos con la realidad y las necesidades del estudiante, tal como lo proponen Penalva et al. (2010). Además, según López et al. (2015), el ABP facilita un aprendizaje más significativo al involucrar a los estudiantes en situaciones con-textualizadas. Asimismo, Vargas et al. (2021) destacan que este enfoque promueve habilidades de resolución de problemas y pensamiento crítico. Finalmente, García y Martínez (2016) enfatizan que la metodología ABP favorece la comprensión conceptual al aplicar los conocimientos en proyectos reales.
Referencias Bibliográficas
Barrera Mesa, M., Fernández Morales, F. H., & Duarte, J. E. (2017). Aprendizaje basado en proyectos colaborativos mediados por TIC para el desarrollo de competencias en estadística. Saber, Ciencia y Libertad, 12(2), 220-232. doi:https://doi.org/10.18041/2382-3240/saber.2017v12n2.1590
Bernal, C. A. (2016). Metodología de la investigación (4ª ed.). Pearson Educación.
Bueno, P. (2018). Aprendizaje basado en problemas (ABP) y habilidades de pensamiento crítico¿ una relación vinculante? Revista Electrónica Interuniversitaria de formación del profesorado, 21(2), 91-108. Obtenido de https://revistas.um.es/reifop/article/view/323371
Cohen, L., & Manion, L. (1990). Métodos de investigación educativa. España: Editorial: La muralla S.A.
Díaz-Barriga, F. (2013). Estrategias docentes para un aprendizaje significativo: Una interpretación constructivista (4ª ed.). McGraw-Hill.
Espinoza, M., & Sánchez, S. (2014). Aprendizaje basado en problemas para enseñar y aprender estadística y probabilidad. Paradigma, 35(1), 103-128. Obtenido de https://ve.scielo.org/scielo.php?script=sci_arttext&pid=S1011-22512014000100005
Franklin, C., Kader, G., Mewborn, D., Moreno, J., Peck, R., Perry, M., & Schaeffer, R. (2007). Guidelines for Assessment and Instruction in Statistics Education (GAISE) Report: A Pre-K–12 Curriculum Framework. American Statistical Association.
García, L., & Martínez, A. (2016). El ABP en el aula de matemáticas: una revisión teórica. Revista Latinoamericana de Investigación en Matemática Educativa, 38-49.
Godino, J. D. (2011). Bases teóricas de la educación estadística. Universidad de Granada.
Hernández-Sampieri, R. (2014). Metodología de la investigación (6ª ed.). México: McGraw-Hill.
López, M., Fernández, J., & Pérez, G. (2015). Aprendizaje basado en proyectos en estadística: Un enfoque innovador. Revista de Educación Matemática, 35(2), 112–125.
López, N. (2015). La enseñanza de la estadística en educación primaria en América Latina. REICE: Revista iberoamericana sobre Calidad, Eficacia y Cambio en Educación, 13(1), 103-121. Obtenido de https://dialnet.unirioja.es/servlet/articulo?codigo=5122347
Penalva, M., Posadas, J., & Roig, A. (2010). Resolución y planteamiento de problemas: Contextos para el aprendizaje de la probabilidad. Educ. mat, 22(3), 23-54.
Schultz, N., & Christensen, H. (2004). Seven-step problem-based learning in an interaction design course. European Journal of Engineering Education, 29(4), 533-541.
Vargas, J. D., Arregocés, I. C., Solano, A. D., & Peña, K. K. (2021). Aprendizaje basado en proyectos soportado en un diseño tecno-pedagógico para la enseñanza de la estadística descriptiva. Formación Universitaria, 14(6), 77–86. doi:https://doi.org/10.4067/S0718-50062021000600077
Vásquez, C., & Alsina, A. (2014). Enseñanza de la Probabilidad en educación primaria. Un desafío para la formación inicial y continua del profesorado. Vásquez, C., & Alsina, A. (2014). Enseñanza de la Probabilidad en educación primaria. Un desafío para la formación inicial y continua del profesorado. Números, 85(1), 5-23., 85(1), 5-23. Obtenido de https://lc.cx/OwBda9
Declaración de conflicto de intereses
Los autores declaran no tener conflictos de intereses.
© 2024 Pineda Procel, J. H., Alban Alcívar, J. A., Cañar Cuenca, J. Y., Jiménez Ordóñez, H. D., & Quezada Yaguachi, D. A.
Este es un artículo de acceso abierto distribuido bajo la licencia Creative Commons de Atribución No Comercial 4.0, que permite su uso sin restricciones, su distribución y reproducción por cualquier medio, siempre que no se haga con fines comerciales y el trabajo original sea fielmente citado.